Skyqyzm

编译原理笔记1


写于：2024-08-21   改于：2024-12-02
字数：3429  阅读需要19 mins

1 导论

编译是将程序设计语言翻译为机器语言的过程。本课程是为了了解PL的基本要素、工作原理、语言翻译的基本方法。 一般把汇编翻译为机器语言称为汇编，把高级语言翻译为汇编或机器指令成为编译。高级语言之间变化称为转换。逆向称为反汇编，反编译

编译与解释

  • 编译：先翻译后执行——C的编译
  • 解释：边翻译边执行——Python解释器

高级语言主要成分

  • 语（词）法：表达式，语句，函数等
  • 语义：解释单词符号和语法单位的意义

编译过程

  • 1.词法分析：根据词法规则使用正规式（正则表达式）和有限自动机（有限状态机）将程序拆解为基本元素。
  • 2.语法分析：判断语法是否正常（连词成句？）
  • 3.语义分析与中间代码生成：根据语法分析的结果分析含义（语句是否通顺），并进行初步翻译，产生中间代码（一种语言）。
  • 4.代码优化：编译器级别的优化，针对中间代码。

  • 5.目标代码生成：翻译中间代码为目标代码。

  • 另外的元素
    • 表格管理：维护代码中元素的内容。
    • 出错处理：try{...}catch(error e)，包括语法错误和语义错误。（拼写错误和语句不通顺）。

2 词法分析

2.1 概述

程序中的记号分为以下五类：

  • 关键字；
  • 标识符：函数，变量等用户自定义内容；
  • 字面量：数值，字符串等；
  • 运算符；
  • 分界符：标点符号；

对于某个记号，包含2个部分，类别与别的信息，为了便于区分，称记号的类别为记号，其他信息称为属性。

词法分析器功能与工作方式

功能：

  • 识别单词符号翻译为单词
  • 删除无用字符
  • 删除注释
  • 词法检查（拼写错误）

工作方式

  • 1.直接翻译为记号流：设计简单，效率高，可移植性好；输出占用内存大；
  • 2.作为语法分析器的子程序执行，共同维护符号表：易于实现；
  • 3.与语法分析器并行执行：维护记号流队列；

源程序的输入与预处理

输入：双缓存区； 预处理：删去无用字符与注释；

2.2 模式的形式化描述(正规式)

定义： 语言L是有限字母表∑上有限长度的字符串的集合。 字母表是符号的非空有限集合，字符串是符号的有穷序列。 子串是原串在前或后删去>=0个字符的部分。 $\epsilon$ 表示长度为0的字符串

对于字符串的基本运算

$X^R$ 表示逆转；

$xy$ 表示java中的 $x+y$ ；

$x \mid y$ 表示java中的 $x \space or \space y$

$x^n$ 表示x重复n次， $x^0 = \epsilon$

$x^*$ 表示x重复大于等于0次的字符串的集合，即 \(x^* = \{ x^0 , x^1 ,...\}\) ;

\[x^* == x^+ | \epsilon\]

运算的预先级为*,+(连接运算),|;

例 2.7 令 $r={d,.,e,+,-}$ ，其中 $d$ 为 $0 \sim 9$ 的数字，则 $r$ 上表示的无符号数的集合的正规式为:

\[d^* (dd^* | \epsilon)(e(+|-|\epsilon)dd^* |\epsilon)\]

对于该式的解析： 第一个 $d^$ 表示数值位至少有一位， $(dd^ | \epsilon)$ 表示0到n位的数值位，e是指数标识符， $(+|-|\epsilon)$ 表示指数符号， $e(+|-|\epsilon)dd^*$ 是有指数时的字符串。

$L(x)$ 指正则表达式对应的集合；

正规式的简化： 1.简化正规式描述

\[x^* = x^+ | \epsilon\] \[r?=r|\epsilon\] \[L([abc]) = \{a|b|c\}\] \[[0-9a-z] = [012...789abc...xyz]\] \[\Sigma = \{a,b,c,d,e,f,g,h\} , L([\space \^{} abc]) = \{d,e,f,g,h\}\]

2.引入辅助定义式（变量）

\[char=[a-z\space A-Z]\] \[digit=[0-9]\] \[digits=digits^+\] \[optional\_ fraction=(. digits)?//纯小数\] \[optional\_ exponent=(E(+|-)?\space digits)?//整数\] \[id=char(char|digit)//首位为字母开头的id字符串\] \[num=digit\space optional\_ fraction\space optional\_ exponent//数字字符串\]

2.3 记号的识别——有限自动机

NFA

NFA（Nondeterministic Finite Automata，不确定的有限自动机） M就是这样一个五元组：

M =（S，∑，move，s0，F）

其中：

S:M的状态集合（有限个元素）；

∑:M的字母表，是由有限个字符（可以包括ε）构成的集合。M 仅能接受/识别其中字符；

move:状态转移函数。move(si，ch)=sj 表示 M 处在状态 si 时若遇到输入字符 ch，则转移到（下一）状态 sj。其中 ch 可以是 Σ 中的某个字符（包含 ε，它表示空字符/不需要输入）；

s0:（唯一的）初态/开始状态。s0是S中的元素，代表识别一个记号的开始；

F:终态集/接受状态集。F 是 S 的一个非空子集。识别记号时只要能够到达 F 中某个状态，则认为刚才扫描过的字符串可被 M 接受（即是一个记号）。

提示： （1）从定义可知，一个 NFA 的终态可以不唯一！ （2）转移函数 move 实际上定义了这样一个映射关系：move: S × ∑ → S 【特别注意】 move 函数是一个偏函数（部分函数），即允许在某个状态下，对于某个/些字符没有状态转移——即没有下一状态！

DFA

DFA （Deterministic Finite Automata，确定的有限自动机）是 NFA 的一个特例，它满足下面两条限制：

（1）没有状态具有ε状态转移(ε-transition)，即状态转换图中没有标记ε的边；

（2）对每个状态s和每个字符a，最多有一个下一状态。

相对于 NFA，构成 DFA 的五元组中，其他都与NFA相同，仅仅转移函数 move 所定义的映射变为： move: S × ∑ → S 即 （1）对于给定的一个状态 s 和一个字符 c，其下一状态最多有一个.（即<=1,0个是可以的） （2）对于每个状态，若不读入任何字符，则保持当前状态不变.

2.4 从正规式到语法分析器

一般步骤如下：

  1. 正规式描述
  2. 正规式->NFA(Thompson算法)
  3. NFA->DFA(模拟NFA,子集法)
  4. 优化DFA
  5. DFA->词法分析器

算法2.2 Thompson算法

正规式构造DFA 图一

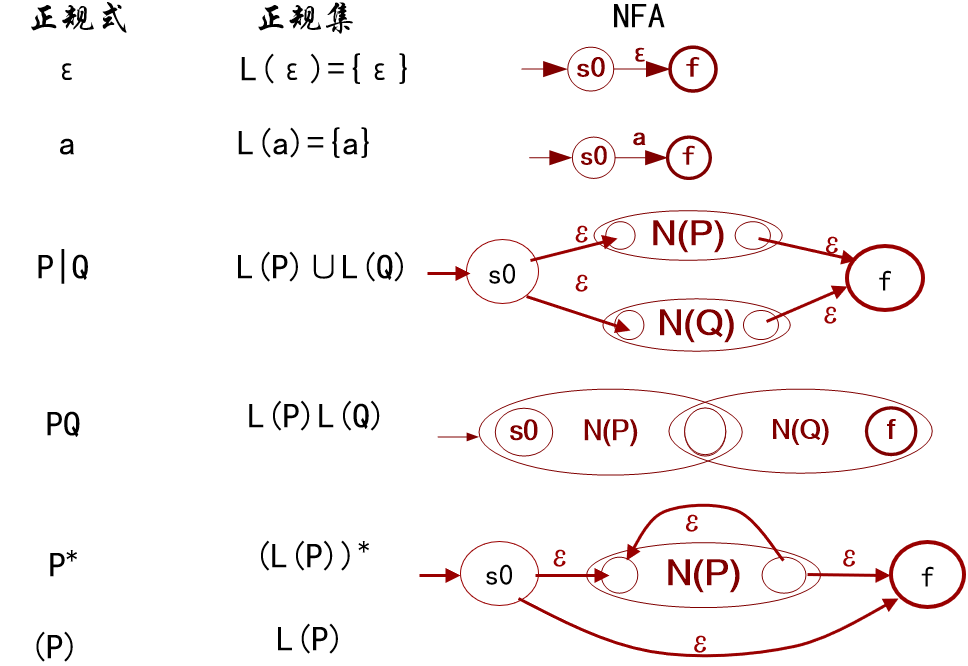
算法2.3 模拟NFA 与 算法2.4 求ε_闭包

有两个概念：

  1. smove(S,a):表示从S开始经过a可以直接到达的下一状态全体
  2. ε_闭包(T):从状态集T出发，不经任何字符（包括空字符ε）可到达的状态全体

算法2.3 模拟NFA

  1. 识别初态集ε_闭包({s0})，令其为A；
  2. 识别输入记号a的ε_闭包(smove(A,a))，不断计算直到输入完成；
  3. 识别路径为Aa…zZ，判断Z中是否存在终态。

例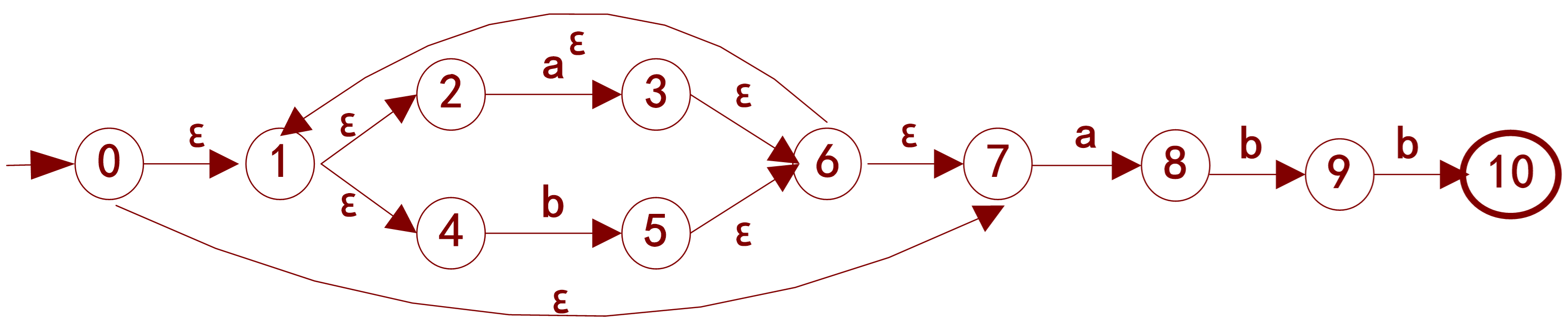： 图二 在NFA上识别输入序列abb和abab：

识别abb:

  1. 计算初态集： ε-闭包({0}) ={0,1,2,4,7}， A
  2. A出发经a到达：ε-闭包(smove(A,a))={3,8,6,7,1,2,4}， B
  3. B出发经b到达：ε-闭包(smove(B,b))={5,9,6,7,1,2,4}， C
  4. C出发经b到达：ε-闭包(smove(C,b))={5,10,6,7,1,2,4}，D
  5. 结束且D∩{10}={10}，接受。 识别的路径为：A a B b C b D

识别abab:

  1. 计算初态集： ε-闭包(s0) ={0,1,2,4,7} A
  2. A出发经a到达：ε-闭包(smove(A,a))={3,8,6,7,1,2,4} B
  3. B出发经b到达：ε-闭包(smove(B,b))={5,9,6,7,1,2,4} C
  4. C出发经a到达：ε-闭包(smove(C,a))={3,8,6,7,1,2,4} B
  5. B出发经b到达：ε-闭包(smove(B,b))={5,9,6,7,1,2,4} C 识别路径为：A a B b C a B b C 因为C∩{10}=Φ所以不接受

算法2.5 子集法构造DFA

  1. 先计算 DFA 的初态，即 ε-闭包 ({s0})，其中 s0 是NFA的初态；
  2. 对于DFA的每一状态，均计算从该状态出发，经过字母表中的每个字符后能够到达的所有状态。这个过程中，会使得 DFA 增加新的状态及状态转移。

与算法2.3比较： 对所有路径进行了确定化

例: 图三 用算法2.5构造(a|b)*abb的DFA：

ε-闭包({0})        ={0,1,2,4,7}       A*
ε-闭包(smove(A, a))={3,8,6,7,1,2,4}   B*
ε-闭包(smove(A, b))={5,6,7,1,2,4}     C*
ε-闭包(smove(B, a))={3,8,6,7,1,2,4}   B
ε-闭包(smove(B, b))={5,9,6,7,1,2,4}   D*
ε-闭包(smove(C, a))={3,8,6,7,1,2,4}   B
ε-闭包(smove(C, b))={5,6,7,1,2,4}     C
ε-闭包(smove(D, a))={3,8,6,7,1,2,4}   B
ε-闭包(smove(D, b))={5,10,6,7,1,2,4}  E*
ε-闭包(smove(E, a))={3,8,6,7,1,2,4}   B
ε-闭包(smove(E, b))={5,6,7,1,2,4}     C

转换矩阵：

/ a b
A B C
B B D
C B C
D B E
E B C

转换图： 图四

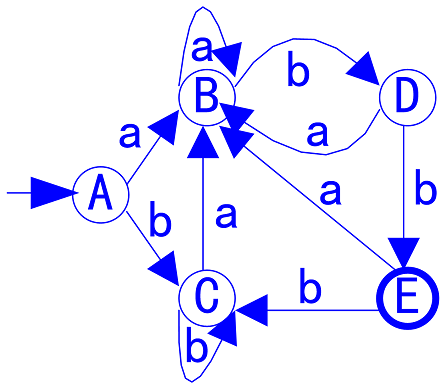
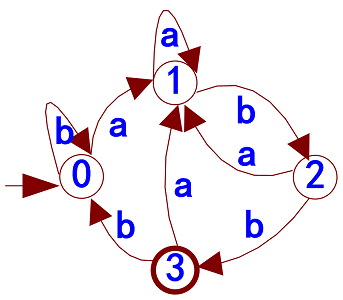
算法2.6 最小化DFA

定义2.8 状态不可区分： 对于任何两个状态t和s，若:

  1. 从一状态出发接受输入字符串ω，而从另一状态出发不接受ω，或者
  2. ∃ω, 从t出发和从s出发到达不同的接受状态， 则称ω对状态t和s是可区分的。

算法：

  1. 先构造一个初始的状态组划分Π={S-F，F}。其中 F 为输入DFA的终态集合，S是该DFA的全部状态构成的集合。
  2. 尝试将Π中的每个状态组进行分裂，得到新的划分Πnew。
    • 若Πnew与Π相同，则分裂结束，并令Πfinal = Πnew，否则
    • 令Π = Πnew，并反复执行此步，直到Πnew与Π 相同。 *这一步要反复利用【状态不可区分】的概念。
  3. 选代表+改转移。针对最终的状态组划分 Πfinal 中的每个状态组，选其中任一状态为该组的代表状态（就是最小DFA的一个状态），将从该组内状态出发的、到达该组内状态的所有状态转移全部替换为该代表状态上的转移。
  4. 删除（可能存在的）死状态、不可达状态。**删除这两类状态时，也应删除与之相关的状态转移。

例： 图五 用算法2.6化简DFA

  1. 初始化划分Π1={ABCD，E}
  2. 根据算法中步骤2，反复分裂划分中的组：
    • ∵ m(D, b)=E ∴ Π2={ABC，D，E}
    • ∵ m(B, b)=D ∴ Π3={AC，B，D，E}
    • Π3？
  3. 于是：Πfinal= Π3 = {AC，B，D，E}
  4. 根据Πfinal构造D’：
    • 选代表，用A代表AC组；
    • 修改状态转移：
/ a b
A B A
B B D
A B A(与A合并)
D B E
E B A

用0、1、2、3 代替A、B、D、E： 图六

Recent posts