编译原理笔记2

3 语法分析

3.1 概述

语法分析器功能：

1. 根据词法分析器提供的记号流，为语法正确的输入构造分析树（或语法树），这是本章的重点；
2. 检查输入中的语法（可能包括词法）错误，并调用出错处理器进行适当处理。

3.2 上下文无关文法(Context Free Grammar,CFG)

3.2.1 定义

定义3.1 CFG 是一个四元组 G =（N，T，P，S），其中

1. N 是非终结符（Nonterminals）的有限集合；
2. T 是终结符（Terminals）的有限集合，且N∩T=Φ；（N是可以出现在产生式左边的符号的集合；T是绝不出现在产生式左边的符号的集合（记号）。）
3. P 是产生式（Productions）的有限集合， A→α，其中A∈N（左部），α∈(N∪T)*（右部）， 若α=ε，则称A→ε为空产生式（也可以记为A →）；
4. S 是非终结符，称为文法的开始符号（Start symbol）。 注： S ∈ N

→读作“定义为”或者“可导出”

文中给出了巴克斯范式（BNF），而实验给出的为扩展的巴克斯范式（EBNF），为文法提供了一定的扩展便于书写。 具体内容见之后博客中总结的内容。

本课程(及考试中)的约定： 大写英文字母A、B、C等表示 非终结符； 小写英文字母a、b、c等表示 终结符； 小写希腊字母α、β、δ等表示 任意文法符号序列。（ ε 除外）

3.2.2 CFG产生语言的基本方法——推导

CFG（产生式）通过推导的方法产生语言，即：

（通俗地讲）从开始符号S开始，反复使用产生式：

将非终结符替换为其产生式右部的文法符号序列(展开产生式，用=>表示)，直到得到一个终结符序列。

定义3.2 利用产生式产生句子的过程中，将 用产生式A→γ的右部替换文法符号序列αAβ中的A得到αγβ的过程 称αAβ直接推导出αγβ，记作：αAβ=>αγβ。

若对于任意文法符号序列α1，α2，…αn，有α1=>α2=>…=>αn，则称此过程为零步或多步推导，记为：

α1=*>αn。其中

若α1=αn ，则称此过程（情况）为零步推导；

若α1≠αn，即推导过程中至少使用一次产生式，则称此过程为至少一步推导，记为：α1=+>αn(箭头上一个加号)。

定义3.3 由 CFG G 所产生的语言 L(G) 被定义为:L(G) = { ω┃S ω and ω∈T* }

L(G)称为上下文无关语言(Context Free Language, CFL)，ω称为句子。

若S≛>α，α∈(N∪T)*，则称α为G的一个句型。

定义3.4 在推导过程中，若每次直接推导均替换句型中最左边的非终结符，则称为最左推导，由最左推导产生的句型被称为左句型。

类似的可以定义最右推导与右句型，最右推导也被称为规范推导。

3.2.3 推导、分析树与语法树

定义3.5 对 CFG G 的句型分析树被定义为具有下述性质的一棵树:

1. 根由开始符号所标记；
2. 每个叶子由一个终结符、非终结符、或ε标记；
3. 每个内部结点由一个非终结符标记；
4. 若A是非叶子节点的标记，且X1，X2，…，Xn是该节点从左到右所有孩子的标记，则A→X1X2…Xn是一个产生式。若A→ε，则标记为A的结点可以仅有一个标记为ε的孩子。

定义3.6 对CFG G的句型，表达式的语法树被定义为具有下述性质的一棵树:

1. 根与内部节点由表达式中的操作符标记；
2. 叶子由表达式中的操作数标记；
3. 用于改变运算优先级和结合性的括号，被隐含在语法树的结构中。

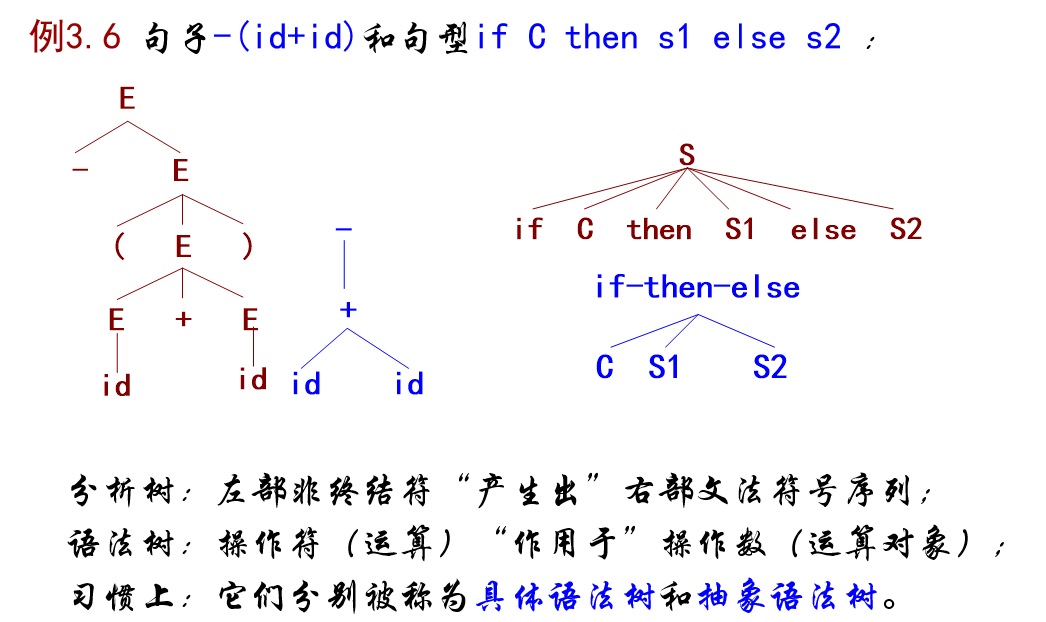
分析树关注产生式推导的过程，而语法树关注运算符计算过程。

3.2.4 二义性与二义性的消除

定义3.7 若文法G对（至少）同一句子产生不止一棵分析树，则称G是二义的。

原因：在产生句子的过程中某些直接推导有多于一种选择

二义性的消除

消除文法二义的两种方法：

① 改写二义文法为非二义文法；

② 规定二义文法中符号的优先级和结合性，使仅产生一棵分析树。

3.3 语言与文法简介

均为概念，做过试卷之后看看是否有必要添加

3.4 自上而下语法分析

3.4.1 自上而下分析的一般方法

对于任何一个输入序列（记号流），从S开始进行最左推导，直到得到一个合法的句子或发现一个非法结构。

特点：

1. 推导过程中，从左到右扫描输入序列，并试图用一切可能的方法，自上而下、自左向右地建立输入的分析树。
2. 自上而下分析是一种试探的过程，是反复使用不同产生式谋求与输入序列匹配的过程。

3.4.2 消除左递归

定义3.9 若文法G中的非终结符A，对某个文法符号序列α存在推导A $\overset{\text{+}}{=}$ >Aα(至少一步推导)，则称G是左递归的。 若G中有形如A→Aα的产生式，则称该产生式对A直接左递归。

算法3.1 消除直接左递归

对于每个含直接左递归的产生式A，首先，整理A产生式为如下形式：

A→ Aα1|Aα2|...|Aαm|β1|β2|...|βn

其中αi非空，βj均不以A开始。然后用下述产生式代替A产生式：

A → β1 A' |β2 A' | ...|βn A'   
A'→ α1 A' | α2 A' | ... | αm A' |ε

算法3.2 消除左递归

输入 无回路文法G 输出 无左递归的等价文法G’ 方法 将非终结符合理排序：A1，A2，…，An;

for(i=2 ; i<n+1 ; i++){
    for(j=1 ; j<i ; j++){
        /*
        #对每个形如Ai→Ajγ产生式中的Aj用Aj→δ1|δ2|...|δk的右部替换,得到新产生式Ai→δ1γ|δ2γ|...|δkγ;
        #消除Ai产生式中的直接左递归;
        */
    }
} 		

核心思想：将无直接左递归的非终结符展开到其他产生式中

例: 用算法3.2消除文法S→Aa|b A→Ac|Sd|ε中的左递归。

1.将S的右部展开在A中，得到：

    A→Ac | Aad | bd | ε

2.消除新产生式中的直接左递归，得到：

    S→ Aa | b
    A→ bdA' | A'
    A'→ cA' | adA' | ε

3.4.3 提取左因子

公共左因子（前缀）：A → αβ1|αβ2

当不确定用A产生式的哪个候选项替换A时，可以重写A的产生式来推迟这种决定，直到看见足够的输入，能正确决定所需选择为止。 这一过程被称为提取左因子，它类似于有限自动机的确定化。

3.4.4 递归下降分析

1. 构造文法的状态转换图并且化简；
   1. 为非终结符A建立一个初态和一个终态；
   2. 为A→X1X2…Xn构造从初态到终态的路径，边标记依次为X1，X2，…，Xn。
2. 将转换图转化为EBNF表示；
   1. 标记为A的边可等价为标记ε的边转向A转换图的初态；
   2. ε边连接的两个状态可以合并；
   3. 标记相同的路径可以合并；
   4. 不可区分的状态可以合并。
3. 从EBNF构造子程序。
   1. { }：重复0或若干次（while）
   2. [ ]：可缺省（if或while）

   3. ：括弧之内的或关系（case）

   4. ( )：改变运算的优先级和结合性

3.4.5 预测分析器

摘自https://www.cnblogs.com/eslzzyl/p/16247421.html

FIRST集合

1. 最简单的情况，A->b，b是终结符。那么FIRST(A)={b}。即终结符的FIRST集合是它本身。

2. 稍复杂一些的情况，A->b

   c

   …

   z，其中b到z都是终结符，那么FIRST(A)={b, c, …, z}。如果这里面有ε，那么把ε也加入FIRST(A)。

3. 更复杂的情况，A->B

   c

   …

   z，其中B是非终结符，c到z是终结符（也可以没有），那么FIRST(A)=FIRST(B){ε}∪{c, …, z}。即所有终结符（如果有）都加入，同时要把FIRST(B)中除去ε（如果有）的部分合并进来。

4. 最复杂的情况，A->B

   C

   …

   Z，其中B到Z都是非终结符。这时要尤其留意ε。如果其中某个非终结符前面所有的非终结符的FIRST集合都包含ε，那么这时将该非终结符的FIRST集合加入FIRST(A)（记得去除集合中的ε）；如果A的所有候选非终结符都能推出ε，那么把ε也加入FIRST(A)。

FOLLOW集合

1. 先看开始符，如果是文法的开始符，则在FOLLOW集合中额外加入#。
2. 在文法的所有推导式的右部寻找A，找到后看紧跟在A后面的字符，设为B。B可以是非终结符，也可以是终结符。如果B是终结符，则直接将B加入FOLLOW(A)（其实是将FIRST(B)加入FOLLOW(A)，但是由于B是终结符，所以FIRST(B)就是B本身）；如果B是非终结符，则将FIRST(B)中除去ε（如果有）的部分加入FOLLOW(A)。如果B只能推导出ε，或A后面根本没有字符，转3。
3. 接2，如果B只能推导出ε，或A后面根本没有字符，则看当前推导式的左部，显然左部是一个非终结符。将这个非终结符的FOLLOW集合加入FOLLOW(A)。
4. 还有一种情况，即2中的B能够推导出ε，但也能推导出其他非空符（即包含ε在内的多个候选）。这时要分开来看，结合2和3。因为B能推导出ε，所以应用规则3，将当前推导式的左部的非终结符的FOLLOW集合加入FOLLOW(A)；因为B还能推导出其他符号，所以应用规则2，将FIRST(B)中除去ε（如果有）的部分加入FOLLOW(A)。这时FOLLOW(A)将是两部分。

/*

个人理解：

First集合是产生式左部的非终结符的集合，注意产生的所有句子中的第一个字符即可。

Follow集合是产生式右部的非终结符的集合，其集合关系较为复杂：对于非终结符右边可能为空时继承产生式左边的Follow集合，右边为非终结符时继承该非终结符的First集合，终结符则加入集合。

*/

例：

L →E;L|ε
E →TE'  
E'→+TE'|-TE'|ε
T →FT'  
T'→*FT'|/FT'|mod FT'|ε
F →(E)|id|num

FIRST(F)  =  {(  id  num }
FIRST(T') =  {*  /  mod  ε}
FIRST(T)  =  FIRST(FT’)={ (  id  num }
FIRST(E') =  {+  -  ε}
FIRST(E)  =  FIRST(TE’) ={ (  id  num }
FIRST(L)  =  FIRST(E;L)∪{ε} ={ (  id  num }

FOLLOW(L)  = { #  }
FOLL0W(E)  = {) ; }
FOLLOW(E') = {) ; }
FOLLOW(T)  = {+  -  ) ; }
FOLLOW(T') = {+  -  ) ; }
FOLLOW(F)  = {*  /  mod  +  -  ) ; } 

预测分析表

1. 对文法的每个产生式(候选项) A→α，执行2和3；
2. 对FIRST(α)的每个终结符a，加入α到M[A，a]；
3. 若ε∈FIRST(α)，则对FOLLOW(A)的每个终结符b(包括#)，加入α到M[A，b]；
4. M中其它没有定义的条目均是error。

3指的是会产生空句子的生成式的处理，即将生成式放到Follow集合中的元素中去。

以上例子的预测分析表为

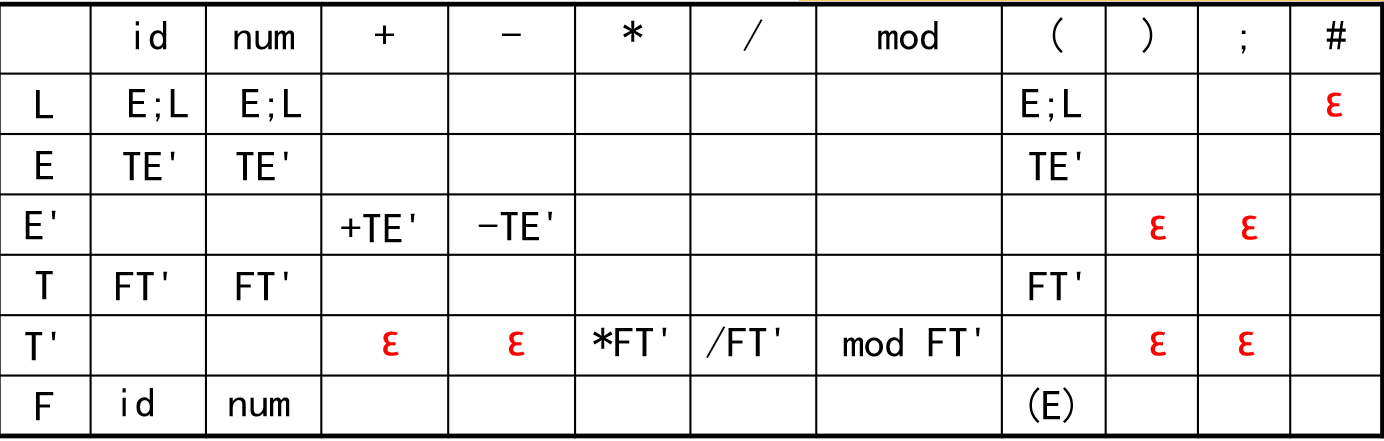
LL(1)文法

定义3.12 文法G被称为是LL(1)文法，当且仅当为它构造的预测分析表中不含多重定义的条目。由此分析表所组成的分析器被称为LL(1)分析器，它所分析的语言被称为LL(1)语言。第一个L代表从左到右扫描输入序列，第二个L表示产生最左推导，1表示在确定分析器的每一步动作时向前看一个终结符。

推论3.2 G是LL(1)的，当且仅当G的任何两个产生式A→α|β满足:

1. 对任何终结符a，α和β不能同时推导出以a开始的串；
2. α和β最多有一个可以推导出ε；
3. 若β=*>ε,则α不能导出以FOLLOW(A)中终结符开始的任何串。

3.5 自下而上分析

定义3.13 设αβδ是文法G的一个句型，

若 存在S=*>αAδ，A=+>β，

则 称β是句型αβδ相对于A的短语。

特别的，若 有A→β，则 称β是句型αβδ相对于产生式A→β的直接短语。

一个句型的最左直接短语被称为句柄。

例：

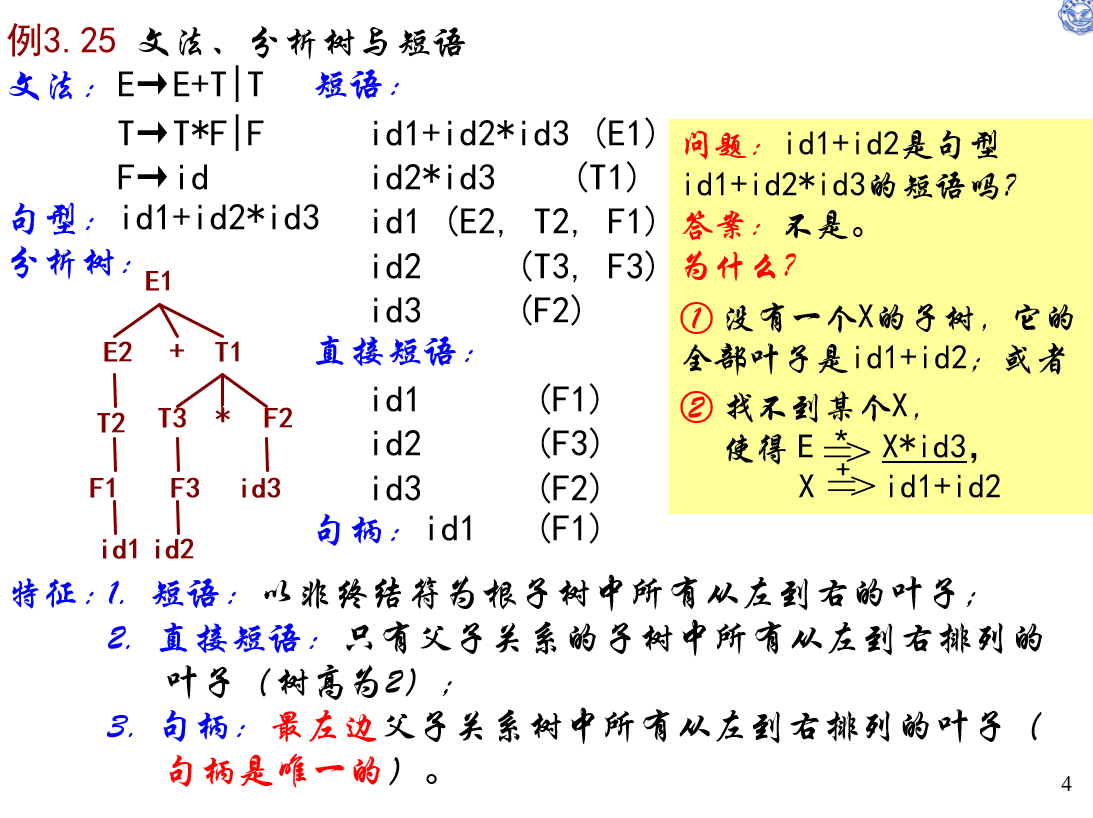
最左/规范归约&剪句柄

最左归约的逆过程是一个最右推导，分别称最右推导和最左归约为规范推导和规范归约。

3.5.2 LR分析

定义3.15 若为文法G构造的移进-归约分析表中不含多重定义的条目，则称G为LR(k)文法，由此分析表构成的分析器被称为LR(k)分析器，它所识别的语言被称为 LR(k)语言。

L 表示从左到右扫描输入序列，R 表示逆序的最右推导，

k 表示为确定下一动作向前看的终结符个数，

一般情况下k<=1。当k=1时，简称LR。